ALJABAR BOOLEAN

ALJABAR BOOLEAN

            Aljabar boolean adalah cabang ilmu matematika yang diperlukan untuk mempelajari desain logika dari suatu sistem digital yang merupakan operasi aritmatik pada bilangan boolean (bilangan yang hanya mengenal 2 keadaan yaitu False/True, Yes/No, 1/0) atau bisa disebut bilangan biner.

Aksioma-aksioma yang berlaku dalam aljabar boolean:

1. Closure :         (i) a + b ϵ B

                        (ii) a ∙ b ϵ B

2. Identitas :        (i) a + 0 = a

                        (ii) a ∙ 1 = a

3. Komutatif :      (i)  a + b = b + a

                        (ii) a ∙ b = b ∙ a

4. Distributif :       (i)  a ∙ (b + c) = (a ∙ b) + (a ∙ c)

                        (ii) a + (b ∙ c ) = (a + b) ∙ (a + c)

5. Komplemen' :   (i)  a + a’ = 1

                               (ii) a ∙ a’ = 0
 

Ekspresi Boolean

Misalkan (B , + , ∙ , ‘) adalah sebuah aljabar boolean.
Suatu ekspresi Boolean dalam (B, + , ∙ , ‘) dapat berbentuk :
(i)     Elemen di dalam B, ex : 0 dan 1
(ii)    Peubah / literal /  variabel, ex : a , b, c
(iii)   Jika e₁ dan e₂ adalah ekspresi Boolean, maka e₁ + e₂ , e₁ ∙ e₂ , e₁’ adalah ekspresi Boolean
Contoh :
a + b
a ∙ b
a’ ∙  (b + c)
a ∙ b’ + a ∙ b ∙ c’ + b’ dsb.

Mengevaluasi Ekspresi Boolean

Contoh :

a’ ∙ (b + c)
Jika a = 0, b = 1 dan c = 0, maka hasil evaluasi ekspresi
0’ ∙ (1 + 0) = 1 ∙ 1 = 1
Dua ekspresi Boolean dikatakan ekivalen (di lambangkan dengan ‘=’) jika keduanya bernilai sama untuk setiap nilai-nilai pada n peubah.
Contoh :

a ∙ (b + c) = (a ∙ b) + (a ∙ c)

-    Catatan : tanda titik (∙) dapat hilang dari penulisan ekpresi Boolean, kecuali :(i)      a(b + c) = ab + ac
(ii)    a + bc = (a + b) (a + c)
(iii)   a ∙ 0 , bukan a0

Prinsip Dualitas

   Missal S adalah kesamaan (identity) di dalam aljabar Boolean yang melibatkan operator +, ∙ , dan komplemen, maka jika pertanyaan S* diperoleh dengan cara mengganti 

      ∙ dengan +

      + dengan ∙

      0 dengan 1

      1 dengan 0
Dan membiarkan operator komplemen tetap apa adanya, maka kesamaan S* juga benar.S*
disebut sebagai dual dari S.
Contoh :
(a ∙ 1)(0 + a’) = 0 dualnya (a + 0 ) + (1 ∙ a’) = 1

Hukum – Hukum Aljabar Boolean

1. Closure:

• (i) a + b ∈ B 
• (ii) a ⋅ b ∈ B 

2. Identitas: 

• (i) a + 0 = a 
• (ii) a ⋅ 1 = a

3. Idempoten: 

• (i) a + a = a 
• (ii) a ⋅ a = a

4. Komplemen:

• (i) a + a’ = 1 
• (ii) aa’ = 0

5. Dominansi: 

• (i) a ⋅ 0 = 0
• (ii) a + 1 = 1 

6. Involusi:

• (i) (a’)’ = a

7. Penyerapan: 

• (i) a + ab = a 
• (ii) a(a + b) = a

8. Komutatif: 

• (i) a + b = b + a 
• (ii) ab = ba

9. Asosiatif:

• (i) a + (b + c) = (a + b) + c 
• (ii) a (b c) = (a b) c

10 Distributif:

• (i) a + (b c) = (a + b) (a + c) 
• (ii) a (b + c) = a b + a c

11. De Morgan: 

• (i) (a + b)’ = a’b’ 
• (ii) (ab)’ = a’ + b’

12. Hukum 0/1:

• (i) 0’ = 1 
• (ii) 1’ = 0

Fungsi Boolean

Fungsi Boolean (fungsi biner) adalah pemetaan dari Bⁿ ke B melalui ekspresi Boolean, :
 f : Bⁿ → B
B adalah himpunan yang beranggotakan pasangan terurut ganda –n (odered n-tuple) di dalam daerah asal B.
Setiap ekspresi Boolean merupakan fungsi Boolean

Contoh :

                        f(x, y, z) = xyz + x’y + y’z

           

fungsi f memetakan nilai nilai pasangan terurut ganda-3 (x,y,z) ke himpunan {0,1}

penyelesaian : (1,0,1) yang berarti x=1, y=0, z=1 sehingga

f(1,0,1) = 1 ∙ 0 ∙ 1 + 1’ ∙ 0 + 0’ ∙ 1 = 0 + 0 + 1 = 1

Bentuk Kanonik

·    Ekspresi Boolean yang menspesifikasikan suatu fungsi dapat disajikan dalam dua bentuk berbeda.

·    Pertama, sebagai penjumlahan dari hasil kali dan kedua sebagai perkalian dari hasil jumlah.

Contoh :

f(x, y, z) = x’y’z + xy’z’ + xyz

dan

g(x, y, z) = (x + y + z)(x + y’ + z)(x + y’ + z’)(x’ + y + z’)(x’ + y’ + z)

adalah dua buah fungsi yang sama.

·    Minterm: suku (term) di dalam ekspresi boolean mengandung literal yang lengkap dalam bentuk hasil kali

·    Maxterm: suku (term) di dalam ekspresi boolean mengandung literal yang lengkap dalam bentuk hasil jumlah.

Contoh :

f(x, y, z) = x’y’z + xy’z’ + xyz -> 3 buah minterm: x’y’z, xy’z’, xyz

g(x, y, z) = (x + y + z)(x + y’ + z)(x + y’ + z’)(x’ + y + z’)(x’ + y’ + z)

-> 5 buah maxterm: (x + y + z), (x + y’ + z), (x + y’ + z’), (x’ + y + z’), dan (x’ + y’ + z)

·    
Misalkan peubah (variable) fungsi Boolean adalah x, y, dan z

Maka:

x’y -> bukan minterm karena literal tidak lengkap

y’z’ -> bukan minterm karena literal tidak lengkap

xy’z, xyz’, x’y’z -> minterm karena literal lengkap

(x + z) -> bukan maxterm karena literal tidak lengkap

(x’ + y + z’) -> maxterm karena literal lengkap

(xy’ + y’ + z) -> bukan maxterm

·    Ekspresi Boolean yang dinyatakan sebagai penjumlahan dari satu atau lebih minterm atau perkalian dari satu atau lebih maxterm disebut dalam bentuk kanonik.

·    Jadi, ada dua macam bentuk kanonik:

1. Penjumlahan dari hasil kali (sum-of-product atau SOP)

2. Perkalian dari hasil jumlah (product-of-sum atau POS)

·       Fungsi f(x, y, z) = x’y’z + xy’z’ + xyz dikatakan dalam bentuk SOP

·       Fungsi g(x, y, z) = (x + y + z)(x + y’ + z)(x + y’ + z’)(x’ + y + z’) (x’ + y’ + z) dikatakan dalam bentuk POS

Cara membentuk minterm dan maxterm:

·    Untuk minterm, setiap peubah yang bernilai 0 dinyatakan dalam bentuk komplemen, sedangkan peubah yang bernilai 1 dinyatakan tanpa komplemen.

·    Sebaliknya, untuk maxterm, setiap peubah yang bernilai 0 dinyatakan tanpa komplemen, sedangkan peubah yang bernilai 1 dinyatakan dalam bentuk komplemen. 

·    Cara membentuk minterm dan maxterm dari tabel kebenaran untuk dua peubah:

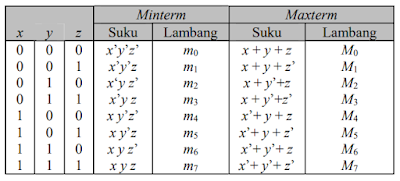
·     Cara membentuk minterm dan maxterm dari tabel kebenaran untuk tiga peubah:

·    Jika diberikan sebuah tabel kebenaran, kita dapat membentuk fungsi Boolean dalam bentuk kanonik (SOP atau POS) dari tabel tersebut dengan cara:

-   mengambil minterm dari setiap nilai fungsi yang bernilai 1 (untuk SOP)

atau

-   mengambil maxterm dari setiap nilai fungsi yang bernilai 0 (untuk POS).